Binary Tree Bin Packing Algorithm

Sat, May 7, 2011

I recently built a ruby gem for auto generating CSS Sprites. It’s simple and flexible, and can be used to generate sprites in either a horizontal or a vertical layout. This works great for most use cases, but has a couple of downsides:

For example, you can see the difference between this:

and this:

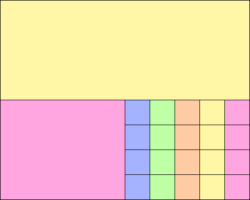
In reality, neither of these issues are very critical. The first issue is really just an annoyance, while the 2nd issue might not be important if we assume that .PNG format images are good at compressing whitespace. Even so, I thought it might be fun to try to implement a bin packing algorithm to generate a more square, packed target file.

Or you can read on to find out…

How it Works

I started by looking up bin packing algorithms in the Algorithm Design Manual:

“Even the most elementary-sounding bin-packing problems are NP-complete. Thus we are doomed to think in terms of heuristics instead of worst-case optimal algorithms.”

Ok, fair enough. Any suggestions ?

“Analytical and empirical results suggest that ‘first fit decreasing’ is the best heuristic. Sort the objects in decreasing order of size, so that the biggest object is first and the smallest last. Insert each object one by one in to the first bin that has room for it.”

Now we’re getting somewhere. Except.. for the purposes of building CSS sprites, I’m not really looking at a pure bin packing algorithm. I only have 1 bin, and I can make it as large as I need. I just need to know:

  1. How to pack the sprites within a single bin.
  2. What is the minimum width and height for the bin to ensure all sprites will fit.

Lets tackle one problem at a time:

Packing Blocks into a Fixed Rectangle

Assuming some arbitrary fixed size, lets say 1024x768, how do we pack rectangular blocks in it ? The answer is to use a binary tree, and a perfect example can be found in the form of Packing lightmaps for game engines.

You start by placing the first (largest) block in the top left corner, then you split that rectangle into 2 smaller rectangles that represent the remaining whitespace:

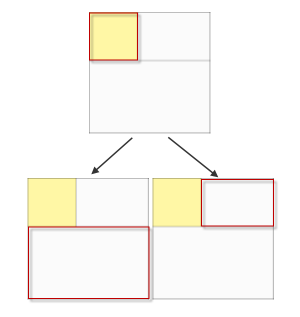
Do this recursively in the form of a binary tree and you end up with a packed image:

The javascript code to do this, assuming the input is already sorted largest to smallest, is surprisingly simple:

Packer = function(w, h) {
  this.root = { x: 0, y: 0, w: w, h: h };
};

Packer.prototype = {

  fit: function(blocks) {
    var n, node, block;
    for (n = 0; n < blocks.length; n++) {
      block = blocks[n];
      if (node = this.findNode(this.root, block.w, block.h))
        block.fit = this.splitNode(node, block.w, block.h);
    }
  },

  findNode: function(root, w, h) {
    if (root.used)
      return this.findNode(root.right, w, h) || this.findNode(root.down, w, h);
    else if ((w <= root.w) && (h <= root.h))
      return root;
    else
      return null;
  },

  splitNode: function(node, w, h) {
    node.used = true;
    node.down  = { x: node.x,     y: node.y + h, w: node.w,     h: node.h - h };
    node.right = { x: node.x + w, y: node.y,     w: node.w - w, h: h          };
    return node;
  }

}

Choosing Minimum Width and Height

We can now use a binary tree for packing small blocks into a fixed size rectangle. But what size should we choose to ensure that all of our sprites fit in as optimal way as possible ?

I considered a number of heuristics. One such example might be to take the average width and average height and multiply by sqrt(n) to try to generate a square:

But any heuristic involving avg is easy to break with a single huge or tiny image and can break down pretty quickly.

Other heuristics are also problematic. So can we take a different approach?

Packing Blocks into a Growing Rectangle

Instead of trying to guess the optimal width and height for a rectangle to pack all of our blocks into, we can start with a small target, just big enough for the first block, and then grow the target as needed whenever there is not enough room for the next block.

Consider a semi packed rectangle where the next block to be packed does not fit:

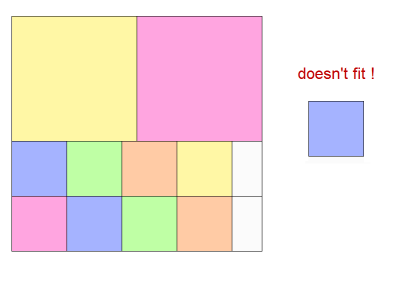
We have 2 choices, we can grow the sprite down, or we can grow to the right:

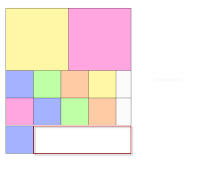
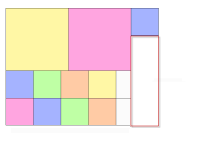
This can be done by adding a couple of new lines to the fit method from the original algorithm:

    fit: function(blocks) {
      var n, node, block;
+     this.root = { x: 0, y: 0, w: blocks[0].w, h: blocks[0].h };
      for (n = 0; n < blocks.length; n++) {
        block = blocks[n];
        if (node = this.findNode(this.root, block.w, block.h))
          block.fit = this.splitNode(node, block.w, block.h);
+       else
+         block.fit = this.growNode(block.w, block.h);
      }
    },

Actually implementing the growNode method involves some more decisions:

    growNode: function(w, h) {
   
 1    var canGrowDown  = (w <= this.root.w);
 1    var canGrowRight = (h <= this.root.h);
   
 2    var shouldGrowRight = canGrowRight && (this.root.h >= (this.root.w + w)); // attempt to keep square-ish by growing right when height is much greater than width
 2    var shouldGrowDown  = canGrowDown  && (this.root.w >= (this.root.h + h)); // attempt to keep square-ish by growing down  when width  is much greater than height
   
      if (shouldGrowRight)
        return this.growRight(w, h);
      else if (shouldGrowDown)
        return this.growDown(w, h);
      else if (canGrowRight)
       return this.growRight(w, h);
      else if (canGrowDown)
        return this.growDown(w, h);
      else
        return null; // need to ensure sensible root starting size to avoid this happening
    },

A couple of notes on (1):

This has a fairly significant impact on the algorithm. If a block appears that is both too wide to grow down and too tall to grow right, then we can’t grow! The solution is to ensure that our blocks are sorted largest first, so that all subsequent blocks will have at least one side smaller than the matching edge of the current target image.

NOTE: It’s not that we can’t support this at all, but the additional complexity required to grow BOTH right and down at the same time is not worth the trouble if we can avoid the problem by sorting our inputs in advance, and performance is not our #1 priority here, so lets do that instead!

A couple of other notes on the code (2):

This prevents us from continuously growing to the right and creating a long horizontal strip. It also prevents us from continuously growing down and creating a narrow vertical strip. It keeps the result roughly square-ish.

See the source code for exact details on how the growRight and growDown methods are implemented.

Sorting the Blocks

The order that the blocks are packed has a significant effect on the results. Lets remind ourselves what the experts say:

“Analytical and empirical results suggest that ‘first fit decreasing’ is the best heuristic. Sort the objects in decreasing order of size, so that the biggest object is first and the smallest last. Insert each object one by one in to the first bin that has room for it.”

What does ‘size’ mean ? height ? width ? area ?

In the demo I allow you to choose from a variety of sorting algorithms.

Each primary sort also has secondary (and sometimes tertiary) sort criteria for blocks that would otherwise be equal.

Subjectively, for the most pleasing square-ish results, the maxside choice is almost always the best choice. It also seems to almost always produce the most effective packing results (e.g. minimal whitespace - reported in the demo as % fit).

Summary

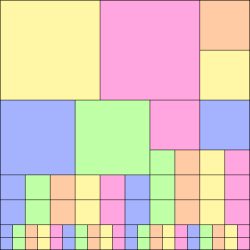
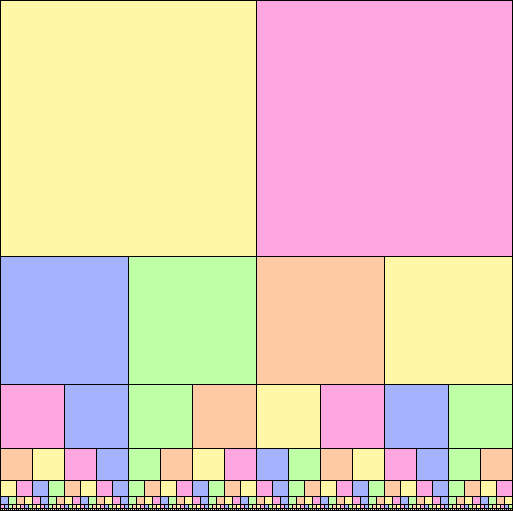
I’m pretty happy with the results. Using the automatic growth algorithm described above, combined with a sort order based on max(width,height) gives me fairly good results for a variety of examples. Where ‘fairly good’ means that the result is roughly square (not long and skinny) and has a minimal amount of whitespace.

Here’s my favorite packing so far, all block sizes are powers of 2…

Next up, implement this packing layout algorithm in ruby for use in the sprite-factory